网易雷火秋招 2023.08.20 机试题目与题解

发表于 2023-08-21 分类于笔试阅读次数：本文字数： 5.8k 阅读时长 ≈ 5 分钟

1、猜数字游戏

雷火小师妹正在参加一个猜数字游戏。游戏规则如下：

系统会随机一个整数作为答案。
小师妹每次可以输入一个猜测的数字。
如果猜测的数字与答案相等，则游戏结束，输出“Congratulations! You guessed it right!”。
如果猜测的数字大于答案，则系统会输出“It's too big, please keep guessing!”。
如果猜测的数字小于答案，则系统会输出“It's too small, please keep guessing!”。
每次小师妹猜测后数值会缩小猜测范围，如果当前猜测的数字在范围之外，则系统会输出“Are you kidding me?”。
小师妹会猜测直到游戏结束，也就是说，小师妹会在最后一次猜测的时候猜对数字。

请你编写一个程序，模拟这个猜数字游戏的过程，并根据小师妹的猜测输出相应的提示信息。

输入

第一行输入一个整数\(n\), 表示小师妹猜测了\(n\)次。（\(1\le n\le 300\)）

接下来输入\(n\)行，每行有一个整数\(a_i\), 表示当前小师妹猜测的数值。

\(1 \le i \le n, 1\le a_i \le 1000\)

输出

根据小师妹猜测的结果，输出相应的提示信息。

样例

输入：
5
10
99
1
40
33

输出：
It's too small, please keep guessing!
It's too big, please keep guessing!
Are you kidding me?
It's too big, please keep guessing!
Congratulations! You guessed it right!

解答

题目已经说明了\(a_n\)是最终答案。因此，一开始我们可以拟定一个足够大的范围，然后按照题意逐渐缩小这个范围并输出对应的提示信息即可。

代码

# include <bits/stdc++.h>
using namespace std;
const int N=304;
int a[N],n;
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    int ans=a[n];
    int l=0,r=1004;
    for(int i=1;i<=n;i++){
        int x=a[i];
        if(x<l||x>r) puts("Are you kidding me?");
        else if(x<ans) puts("It's too small, please keep guessing!"),l=x+1;
        else if(x>ans) puts("It's too big, please keep guessing!"),r=x-1;
        else{
            puts("Congratulations! You guessed it right!");
            break;
        }
    }
}

2、卡牌配置

雷火小师妹最近在攻略某个卡牌游戏，下副本的时候对副本的机制产生了兴趣，希望你帮他算算最优的刷副本方式。

假设小师妹持有A，B两种卡牌，小师妹在副本准备阶段，可以得知这个关卡的地图分布，地图为一个\(n\)行\(m\)列的矩阵格子，每个格子上必须放置且仅能放置一张卡牌。\(0<m,n<6\)。

小师妹可以决定在本关卡中A和B卡牌的配比。

当小师妹决定好A、B卡牌放置数量后，系统会将A、B以随机分布的形式填充到矩阵中。

A卡牌产出为\(0\)，B卡牌产出为\(c\)，\(c\)为正整数。

当B卡牌与A卡牌相邻时(九宫格范围内都算相邻，即八个方向都算)，B卡牌的产出变为原先的\(d\)倍，\(d\)为大于\(1\)的正数。

当B与多个A相邻时，翻倍效果叠加(例如B1与A1，A2，A3同时相邻时，B1的产出是\(c*d*d*d\))。

求问给定\(n,m,c,d\)，当A、B数量分别为多少时产出的期望值最高，期望值是多少？(如果有两种组合期望相同，请输出A卡牌数量较少的那个结果)

下面是一个例子：假设\(n=2,m=2,c=1,d=2\)

说明小师妹将要面临的关卡是个\(2\times2\)的矩阵，

当小师妹决定放置全部使用A卡牌时，很显然这很不明智，产出为\(0\)。

当小师妹决定放置\(1\)个B卡牌，其余使用A卡牌时，系统随机分配时有4种可能：

1 2	BA AB AA AA AA AA BA AB

产出均为\(8(1\times2\times2\times2)\)，所以期望产出为\(8*4/4=8\)。

当小师妹决定放置\(2\)个B卡牌，其余使用A卡牌时，共有\(6\)种可能情况，此时产出均为\(8(1\times2\times2+1\times2\times2)\)，所以期望是\(8\)。

当小师妹决定放置\(3\)个B卡牌，其余使用A卡牌时，也有\(4\)种可能情况，产出均为\(6(1\times2+1\times2+1\times2)\)，所以期望是\(6\)。

当小师妹决定放置\(4\)个B卡牌时，只有一种可能，产出为\(4\)，期望就是\(4\)。

所以最终这个例子的结果是：两种组合期望相同时，选A卡牌数量较少的结果，所以选择放入\(2\)张A卡牌，\(2\)张B卡牌，期望值为\(8.0\)。

输入

一行\(n,m,c,d\)，代表矩阵的行数，矩阵的列数，B卡牌的产出值,A卡牌与B卡牌相邻时对B卡牌产出的影响，\(0<m,n<6\)，\(c\)为正整数\((1\le c \le 100),d\)为大于\(1\)的小数\((1<d<10)\)。

输出

输出一行三个数字，分别代表A卡牌放入数量，B卡牌放入数量，产出的期望值(四舍五入后保留一位小数)，以空格隔开。

如果有两种组合期望相同，请输出A卡牌数量较少的那个结果。

样例

输入：
2 2 1 2

输出：
2 2 8.0

输入：
2 3 1 2

输出：
4 2 18.1

解答

根据期望的线性性质，我们可以求出每个格子所产生的贡献的期望值，然后再将它们相加即可。

更进一步：由于每个格子最多只有\(8\)个邻居，因此这\(nm\)个格子可以分成\(8\)类（可能有\(0,1,\dots,8\)个邻居），每一类只需要计算一次即可，最终乘上这类格子的数量即可。假设\(cnt_i\)表示有\(i\)个邻居的格子的数量。

因此我们现在单独考虑一个格子\(g\)贡献的期望值。假设\(g\)有\(e(e\in\{0,1,2,3,\dots,\min(nm-1,8)\})\)个邻居。我们现在有\(a\)张A卡牌和\(b=nm-a\)张B卡牌。考虑将这些卡牌随机放置后，如下事件的概率\(p(e_a,e_b,a,b)\)：

\(g\)放置的是B卡牌，并且它的邻居中有\(e_a\)个A卡牌，有\(e_b-1=e-e_a\)个B卡牌。

注意，\(e_b\)是\(g\)和它的邻居总共使用的B卡牌数量。\(e_b\)也要满足约束其中\(1\le e_b\le b\)。

在这\(e+1\)个格子中（即\(g\)和它的所有邻居），被分配\(e_a\)个卡牌，\(e_b\)个卡牌的概率是

\(\begin{aligned} &\dfrac{a}{nm}\cdot\dfrac{a-1}{nm-1}\cdot\dfrac{a-2}{nm}\cdot...\cdot\dfrac{a-(e_a-1)}{nm-(e_a-1)}\cdot\dfrac{b}{nm-(e_a-1)-1}\cdot\dfrac{b-1}{nm-(e_a-1)-2}\cdot...\cdot\dfrac{b-(e_b-1)}{nm-(e_a-1)-e_b}\\ =&\dfrac{a!}{(a-e_a)!}\cdot\dfrac{b!}{(b-e_b)!}\cdot\dfrac{(mn-(e_a+e_b))!}{(mn)!}\\ =&\dfrac{a!}{(a-e_a)!}\cdot\dfrac{b!}{(b-e_b)!}\cdot\dfrac{(mn-(e+1))!}{(mn)!} \end{aligned}\)

那么接下来为这些卡片分配位置。由于格子\(g\)一定是放置B卡牌，因此剩下的卡牌可以随意摆放，有\(\dbinom{e}{e_a}\)种放法。因此可以得出

\[p(e_a,e_b,a,b)=\dfrac{a!}{(a-e_a)!}\cdot\dfrac{b!}{(b-e_b)!}\cdot\dfrac{(mn-(e+1))!}{(mn)!}\cdot \dbinom{e}{e_a}\]

因此，最终答案为

\[\sum_{c=0}^8cnt_c\cdot\left(\sum_{\substack{e_a+e_b=e+1;\\0\le e_a\le a;\\ 1\le e_b\le b;}}p(e_a,e_b,a,b)\cdot c\cdot d^{e_a}\right)\]

枚举\(a\)时，只需要按照题意，选计算结果最小的一个即可。

为了保证精度，我这里使用了Python的Fraction来保证避免浮点数误差

代码

from fractions import Fraction
from math import comb

n, m, c, d = input().split()
n, m, c, d = int(n), int(m), int(c), Fraction(d)

cnt = [0 for _ in range(9)]
for i in range(n):
    for j in range(m):
        v = 0
        for dx in [-1, 0, 1]:
            for dy in [-1, 0, 1]:
                x, y = i + dx, j + dy
                if 0 <= x < n and 0 <= y < m:
                    v += 1
        cnt[v - 1] += 1


def solve(a):
    b = n * m - a
    if b == 0:
        return 0
    ans = Fraction(0)
    for e in range(8 + 1):
        if e + 1 > n * m:
            continue
        p = [0 for i in range(e + 1)]
        s = Fraction(0)
        for ea in range(e + 1):
            if ea > a:
                continue
            val = Fraction(1, 1)
            eb = e + 1 - ea
            if eb == 0:
                continue
            for i in range(e + 1):
                val /= n * m - i
            for i in range(ea):
                val *= a - i
            for i in range(eb):
                val *= b - i
            val *= comb(e, ea)
            p[ea] += val
        for ea in range(e + 1):
            s += c * (d ** ea) * p[ea]
        ans += s * cnt[e]
    return ans


ans = []
for a in range(n * m + 1):
    ans.append(solve(a))
mx = max(ans)
for a in range(n * m + 1):
    if ans[a] == mx:
        print(a, n * m - a, "{:.1f}".format(float(mx)))
        break

3、逆水寒匹配

逆水寒是一款大型mmo游戏，战场是其中的核心玩法，如何选出合适的队伍对战是需要考虑的问题。

假设有\(n\)支队伍，每支队伍\(1\)到\(6\)人，这些队伍按先后顺序全部进入匹配池后才开始匹配。现在要求这些队伍匹配组成\(m\)人的团队，并且团队中有且仅有\(1\)个\(a\)职业和\(1\)个\(b\)职业。玩家报名时保证每支队伍中最多只会有\(1\)个\(a\)和\(1\)个\(b\)职业，否则会报名失败。

匹配结果需要满足先进入匹配池的队伍优先组成团队（除非该队伍无法组成团队）。现在要求输出所有符合要求的队伍组合的id, 其中队伍id是指第几个输入的队伍，id从\(1\)开始，id小的队伍会先进入匹配池。

输入

每组用例第一行为参数设置，一共4个整数：

\(n(1\le n\le 1000)\)表示总报名队伍数，\(m(6\le m\le 24)\)表示匹配后的团队总人数，\(a(1\le a\le 8)\)和\(b(1\le b\le 8)\)为职业参数，并且保证\(a\)不等于\(b\)。

紧接着有\(n\)行，第\(i(1 \le i \le n)\)行先是一个数字\(t(1\le t\le 6)\)表示id为\(i\)的队伍中有\(t\)个玩家，该行后续的\(t\)个数字表示该队伍每个玩家的职业。

输出

按先进入匹配池的队伍优先组成团队的规则，按顺序输出所有符合要求的队伍id组合，每个组合一行，队伍id之间用空格隔开。

样例

输入：
6 6 1 2
1 1
2 2 3
5 3 3 3 4 2
3 4 5 6
1 1
1 2

输出：
1 2 4
3 5

提示：
不选1 3和2 4 5的原因：本题要优先保证先进入匹配池的队伍优先组成团队，2比3优先级高，并且1 2能拉上后面的队伍凑出符合要求的团队。

解答

本题主要通过搜索来进行解决。

可以发现，所有队伍可以划分成\(24\)种不同类型：按照队伍人数，队伍是否含有\(a\)职业，是否含有\(b\)职业。由于一个队伍最多只有\(6\)个人，因此一共可以划分成\(6\times 2\times 2=24\)类队伍。

如果当前最优先进入匹配池的队伍是\(i\)（这意味着剩余队伍的编号都大于\(i\)），并且队伍\(i\)没有办法组成一个团队，那么和\(i\)同类的所有团队也必定无法进行组队，这一类的队伍可以删去，来减小搜索时间。

最终，每一次搜索最多只有\(24\)个分支（而不是暴力地产生出\(O(n)\)个分支），记录这\(24\)类不同的队伍中的最小队伍编号（这里比较随机，使用了双端队列来实现），从小到大遍历这些最小队伍编号再进行下一轮的搜索即可。

如果组好了队，那么需要将已经组好的队伍删去。

代码

# include <bits/stdc++.h>
using namespace std;
const int N=1004;
deque<int>g[14][2][2];
int c[N],ha[N],hb[N],vis[N];
vector<int>now;
int n,m,a,b;
struct P{
    int c,oka,okb;
};
bool dfs(int c,int oka,int okb){
    if(c>m) return 0;
    if(c==m){
        if(!oka||!okb) return 0;
        else return 1;
    }
    map<int,P>mp;
    for(int i=1;i<=6&&c+i<=m;i++){
        for(int j=0;j<2;j++){
            for(int k=0;k<2;k++){
                if(oka&&j||okb&&k||g[i][j][k].empty()) continue;
                mp[g[i][j][k].front()]=P{i,j,k};
            }
        }
    }
    for(auto &[id,p]:mp){
        g[p.c][p.oka][p.okb].pop_front();
        now.push_back(id);
        if(dfs(c+p.c,oka|p.oka,okb|p.okb)) return 1;
        g[p.c][p.oka][p.okb].push_front(id);
        now.pop_back();
    }
    return 0;
}
int main(){
    scanf("%d %d %d %d",&n,&m,&a,&b);
    for(int i=1;i<=n;i++){
        int m,t,oka=0,okb=0;
        scanf("%d",&m);
        for(int i=1;i<=m;i++){
            scanf("%d",&t);
            if(t==a) oka=1;
            if(t==b) okb=1;
        }
        c[i]=m;
        ha[i]=oka;
        hb[i]=okb;
        g[m][oka][okb].push_back(i);
    }
    for(int i=1;i<=n;i++){
        if(vis[i]) continue;
        now={i};
        g[c[i]][ha[i]][hb[i]].pop_front();
        if(dfs(c[i],ha[i],hb[i])){
            for(int i=0;i<now.size();i++){
                vis[now[i]]=1;
                printf("%d%c",now[i], " \n"[i+1==now.size()]);
            }
        }
        else{
            for(int x:g[c[i]][ha[i]][hb[i]]){
                vis[x]=1;
            }
            g[c[i]][ha[i]][hb[i]].clear();
        }
    }
}

4、家园水池数据存储

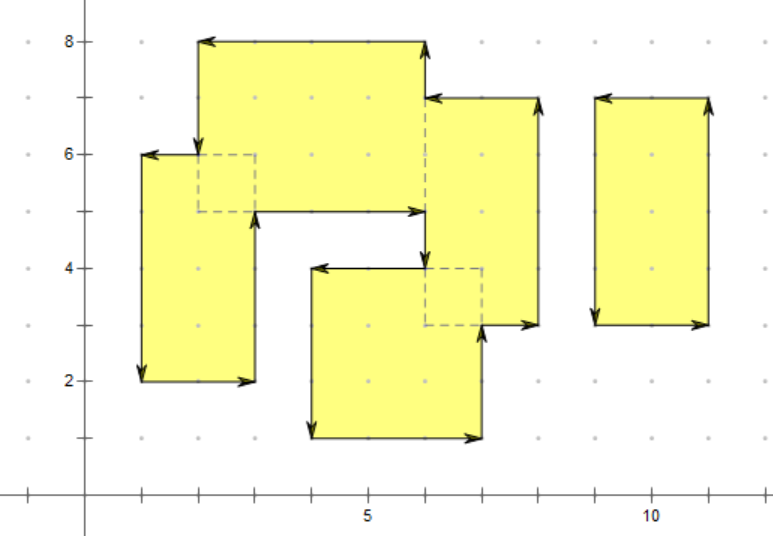
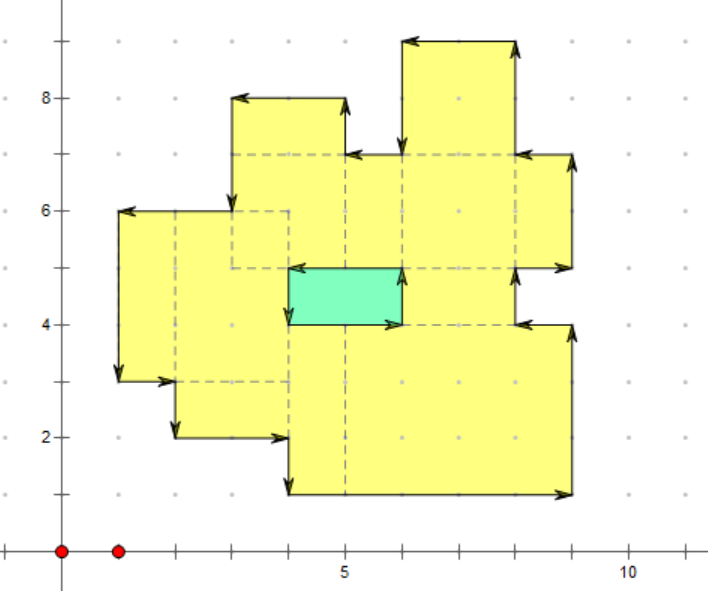
《新倩女幽魂》最近正在迭代家园玩法，新增了一个家园建造水池的功能，玩家可以多次使用自定义大小的矩形生成水池区域。小倩为了记录水池形状，需要从左下角的顶点（优先x坐标最小，其次y坐标最小的点），以逆时针的顺序依次记录水池边的顶点。玩家可能会生成多组不连通的水池（图1的1和2），需要分别记录（输出时分行表示不连通的水池）；玩家建造的水池可能会形成内陆，也需要分行输出内陆边缘的信息（图2的2和3）。

图1 多组不连通水池的情况

图2 拼接水池存在内陆的情况为了美观考虑，小倩不允许玩家在编辑水池时出现矩形之间只有一个交点的情况，如图3所示。

图3 不允许出现多个矩形之间只有一个交点的情况

输入

每组数据首行输入整数\(n(1\le n\le 1000)\)，表示玩家使用矩形编辑场景的次数。接下来输入\(n\)行数据，每行有四个整数\(x_1,y_1,x_2,y_2(0\le x_1, y_1, x_2, y_2\le 100000，x_1<x_2, y_1< y_2)\)，用空格分割，表示矩形左下角\((x_1,y_1)\)与右上角\((x_2,y_2)\)的坐标。

输出

每组数据输出玩家编辑水池后，生成的连通图顶点信息。每组连通图数据单独成行，起始点为左下角（优先\(x\)坐标最小，其次\(y\)坐标最小，下同），以逆时针方向依次输出，\(x,y\)坐标与各个顶点之间的数据以空格分割；多组连通图的顺序以起始点更靠左下角的顺序输出。

样例

输入：
5
1 2 3 6
2 5 6 8
6 3 8 7
4 1 7 4
9 3 11 7

输出：
1 2 3 2 3 5 6 5 6 4 4 4 4 1 7 1 7 3 8 3 8 7 6 7 6 8 2 8 2 6 1 6
9 3 11 3 11 7 9 7

输入：
7
1 3 4 6
2 2 4 6
3 5 5 8
3 5 9 7
6 4 8 9
5 1 9 4
4 1 9 4

输出：
1 3 2 3 2 2 4 2 4 1 9 1 9 4 8 4 8 5 9 5 9 7 8 7 8 9 6 9 6 7 5 7 5 8 3 8 3 6 1 6
4 4 6 4 6 5 4 5

（注：以下两张图分别对应了这两个测试用例的答案，原题没有这两张图）

解答

这道题，实在无力吐槽，需要考察的东西实在太多了。以下按步骤详述每个过程。

1、坐标离散化

可见坐标数据范围达到了\(10^5\)，为了能够只需要\(O(n^2)\)空间就能争取地展示出这个矩形的形状，我们需要对这些坐标进行离散化。由于这题需要考虑所有网格的边界和它相邻的所有邻居，并且为了正确处理边界坐标，这里对于输入中每个包含的\((x,y)\)坐标，\(x-1,x,x+1,y-1,y,y+1\)都要插入待离散化的坐标中。

最终我们可以将这个网格图的坐标压缩到\(6000\)以内，可以使用一个二维数组进行存储。

2、求出地图

接下来则是求出这个离散化后的具体地图\(d\)的形状。对于每一个离散化后的坐标\(x_1,y_1,x_2,y_2\)（注意，离散化后，我们的所有坐标都用格子坐标表示，每个格子的坐标和它左下角顶点的坐标相等），一个朴素的办法是对\(s\)中所有满足\(x_1\le x\le x_2,y_1\le y\le y_2\)的坐标都填上\(1\)。但是每次填充一个矩形都要\(O(n^2)\)的时间，如果\(n\)个矩形都这样填充，那么会导致超时。一个解决办法是求取二维差分数组，然后再使用二维前缀和的方法可以在\(O(n^2)\)求出一个01地图\(s\)。

3、重新化格子坐标为点坐标

对于一个格子\((x,y)\)，它的左下角的点坐标为\((x,y)\)，右下角的点坐标为\((x+1,y)\)，左上角的点坐标为\((x,y+1)\)，右上角的点坐标为\((x+1,y+1)\)。

如果这个格子和左边的格子不相同，那么点\((x,y)\)与点\((x,y+1)\)有一条边界线。同样的，如果这个格子和左边的格子不相同，那么点\((x,y)\)与点\((x+1,y)\)有一条边界线。为了方便，我们使用一个\(4\)比特元素的数组\(g\)，来存储每个点朝哪个方向有一条边界线。

4、求出每条边界

根据\(g\)数组，可以知道一个坐标点是否在某条边界上。按顺序枚举\(x\)坐标最小，如果有多个点相同，\(y\)坐标最小的点\((x_0,y_0)\)，按照\(g\)数组沿着这条边界环绕一圈，并记录所有转弯处的节点即可。这条边界就是题目所求的边界。需要注意的有以下三点：

为了避免重复枚举，所有点经过一次后都需要进行标记。
由于\((x_0,y_0)\)是“\(x\)坐标最小，如果有多个点相同，\(y\)坐标最小的点\((x_0,y_0)\)”的点，并且现在需要逆时针方向遍历所有节点，因此一开始沿着的方向是向右遍历。
枚举完所有节点后，需要将离散化后的坐标映射回离散化前的坐标再输出。

代码

# include <bits/stdc++.h>
# define pi pair<int,int>
# define X first
# define Y second
using namespace std;
const int N=6004;
struct Rec{
    int xa,ya,xb,yb;
}r[N];
int n;

map<int,int>mpx,mpy;
int raw_x[N],raw_y[N];
int mx=0,my=0;

int s[N][N];
char g[N][N], vis[N][N];

const int L=0,R=2,U=1,D=3;

void gen_dir(){
    for(int x=1;x<=mx;x++)
        for(int y=1;y<=my;y++){
            if(s[x][y]!=s[x-1][y]){
                g[x][y]|=1<<U;
                g[x][y+1]|=1<<D;
            }
            if(s[x][y]!=s[x][y-1]){
                g[x][y]|=1<<R;
                g[x+1][y]|=1<<L;
            }
        }
}
vector<pi>gen_path(int sx,int sy){
    vector<pi>ans{pi(raw_x[sx],raw_y[sy])};
    int dir=R;
    for(int x=sx,y=sy;;){
        if(dir==R){
            while(g[x][y]>>R&1) vis[x][y]=1,++x;
            dir=(g[x][y]>>U&1?U:D);
        }
        else if(dir==L){
            while(g[x][y]>>L&1) vis[x][y]=1,--x;
            dir=(g[x][y]>>U&1?U:D);
        }
        else if(dir==U){
            while(g[x][y]>>U&1) vis[x][y]=1,++y;
            dir=(g[x][y]>>L&1?L:R);
        }
        else if(dir==D){
            while(g[x][y]>>D&1) vis[x][y]=1,--y;
            dir=(g[x][y]>>L&1?L:R);
        }
        if(x==sx&&y==sy) break;
        else ans.push_back(pi(raw_x[x],raw_y[y]));
    }
    return ans;
}
int main(){
    scanf("%d",&n);
    int xa,ya,xb,yb;
    for(int i=1;i<=n;i++){
        scanf("%d %d %d %d",&xa,&ya,&xb,&yb);
        --xb;--yb;
        r[i]=Rec{xa,ya,xb,yb};
        mpx[xa]=mpx[xb]=0;
        mpy[ya]=mpy[yb]=0;
        mpx[xa-1]=mpx[xb-1]=0;
        mpy[ya-1]=mpy[yb-1]=0;
        mpx[xa+1]=mpx[xb+1]=0;
        mpy[ya+1]=mpy[yb+1]=0;
    }
    for(auto &[k,v]:mpx){
        v=++mx;raw_x[mx]=k;
    }
    for(auto &[k,v]:mpy){
        v=++my;raw_y[my]=k;
    }
    for(int i=1;i<=n;i++){
        xa=mpx[r[i].xa];ya=mpy[r[i].ya];
        xb=mpx[r[i].xb];yb=mpy[r[i].yb];
        r[i]=Rec{xa,ya,xb,yb};
        s[xa][ya]++;s[xa][yb+1]--;
        s[xb+1][ya]--;s[xb+1][yb+1]++;
    }
    for(int i=1;i<=mx;i++){
        for(int j=1;j<=my;j++){
            s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
        }
    }
    for(int i=1;i<=mx;i++)
        for(int j=1;j<=my;j++)
            if(s[i][j]) s[i][j]=1;
    gen_dir();
    for(int x=1;x<=mx;x++)
        for(int y=1;y<=my;y++)
            if(!vis[x][y]&&g[x][y]){
                vector<pi>p=gen_path(x,y);
                for(int k=0;k<p.size();k++)
                    printf("%d %d%c",p[k].X,p[k].Y," \n"[k+1==p.size()]);
            }

}